第一大题
1.1
分支限界法和回溯法的区别及相同点?
求解目标不同:
- 回溯法的求解目标是找出解空间树中满足约束条件的所有解
- 分支限界法的求解目标是找出满足约束条件的一个解,或是在满足约束条件的解中找出在某种意义下的最优解
搜索方式不同:
- 回溯法以深度优先的方式搜索解空间树
- 分支限界法以广度优先或以最小耗费优先的方式搜索解空间树
相同点:
- 均基于解空间树搜索;采用剪枝优化搜索效率。
1.2
数学建模。
- 问题转化:将环保投资问题建模为 0-1 背包问题模型。
- 变量定义:$x_i \in \{0,1\}$ 表示是否投资第 $i$ 个方案(1=投资,0=不投资)。
- 目标函数:最大化总减碳量 $\max \sum_{i=1}^{3} v_i x_i$($v_i$ 为减碳量)。
- 约束条件:总成本 $\sum_{i=1}^{3} w_i x_i \leq 30$($w_i$ 为成本)。
- 结论:减碳量等效为背包"价值",成本等效为"重量",投资上限 30 等效为背包容量。
队列式分支限界法求解过程?最大减碳量?最优方案组合?
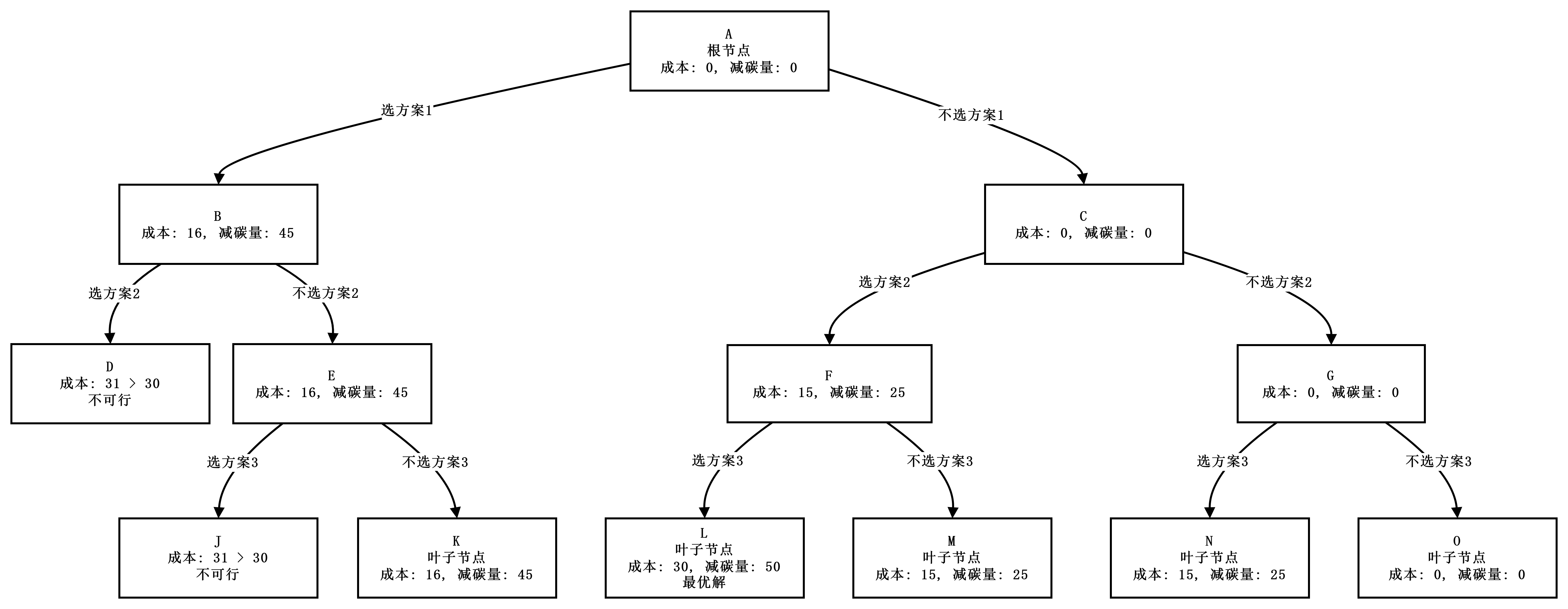
- 构造解空间树:三层二叉树(左分支=选方案,右分支=不选方案)。
-
搜索过程:
[A] B, C => B, C [B, C] D, E => E [C, E] F, G => F, G [E, F, G] J, K => K(45)[1,0,0] [F, G] L, M => L(50)[0,1,1], M(25)[0,1,0] [G] N, O => N(25)[0,0,1], O(0)[0,0,0] - 最优值(最大减碳量):50 万吨
- 最优解(最优方案组合):选方案 2 和方案 3,即 $x = [0,1,1]$
1.3
回溯法编程实现,找这个方案的最大减碳量以及最优方案组合。
[回溯函数]
void Backtrack(int i) {
// 如果到达叶子节点
if (i > n) {
bestp = cp;
return;
}
// 进入左子树
if (cw + w[i] <= c) {
cw += w[i];
cp += p[i];
Backtrack(i + 1);
cw -= w[i];
cp -= p[i];
}
// 进入右子树
if (Bound(i + 1) > bestp) {
Backtrack(i + 1);
}
}[限界函数]
private static double Bound(int i) {
// 计算剩余容量
double cleft = c - cw;
double bound = cp;
// 以物品单位重量价值递减序装入物品
while (i <= n && w[i] <= cleft) {
cleft -= w[i];
bound += p[i];
i++;
}
// 装满背包
if (i <= n) {
bound += p[i] / w[i] * cleft;
}
return bound;
}第二大题
2.1
贪心算法的原理是什么?
- 贪心算法是一种通过局部最优选择来构建全局最优解的算法。
- 它依赖于贪心选择性质和最优子结构,即每一步都选择当前最优,期望最终得到全局最优解,且无需回溯。
哈夫曼编码原理是什么?
- 变长编码:哈夫曼编码是一种变长编码方式。出现频率高的字符分配较短的编码,出现频率低的字符分配较长的编码。
- 频率排序:首先将字符按照出现频率从小到大排序。
-
构造哈夫曼树:
- 每次选取频率最小的两个节点。
- 创建一个父节点,其频率等于这两个子节点频率之和。
- 将该父节点按照频率大小重新插入到排序好的节点队列中。
- 重复以上步骤,直到队列中只剩下一个节点,这个节点就是哈夫曼树的根节点。
-
编码:在哈夫曼树上,左分支编
0右分支编1,直到到达叶子节点,路径上的0和1组成的字符串就是该字符的哈夫曼编码。
定长编码的原理是什么?
定长编码也称为等长编码,是一种数据编码方式,其中每个字符或符号都用固定长度的二进制位来表示。
定长编码计算方式:
- 确定字符集大小 $N$(需编码的不同字符总数)。
-
计算最小编码位长 $L$:$2^L \geqslant N$
- 等价对数形式:$L = \lceil \log_2 N \rceil$,其中 $\lceil \cdot \rceil$ 表示向上取整函数。
2.2
构造哈夫曼树及编码,写出具体的构造过程,写出每种垃圾名称的具体编码。
垃圾类型由小到大排序:
| 4 | 3 | 2 | 1 |
|---|---|---|---|
| 其他垃圾 | 有害垃圾 | 厨余垃圾 | 可回收垃圾 |
| 10% | 15% | 30% | 45% |
构造哈夫曼树:
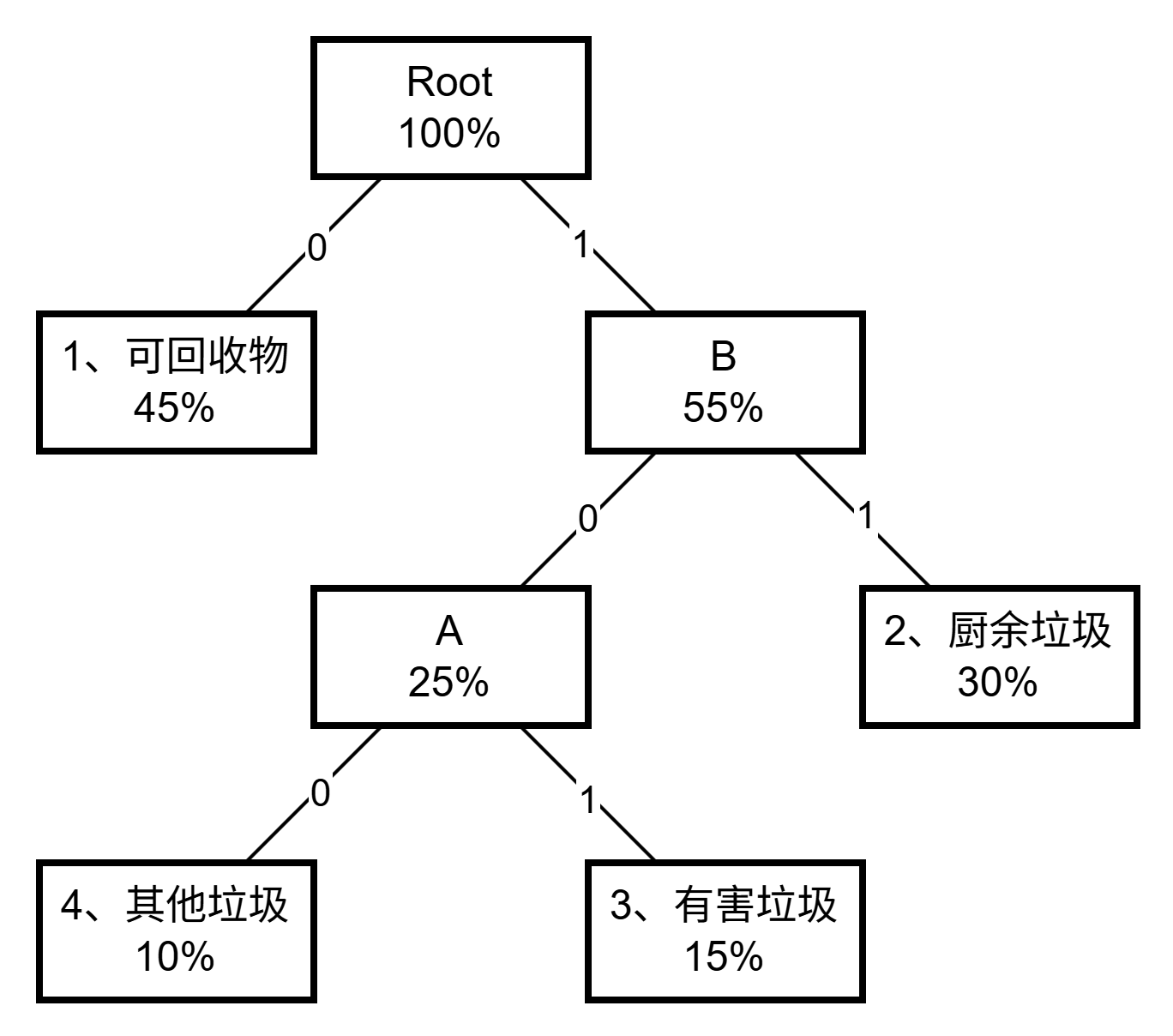
根据哈夫曼树可得:
- 可回收物:
0 - 厨余垃圾:
11 - 有害垃圾:
101 - 其他垃圾:
100
2.3
编码长度与节省比例计算
-
定长编码:
- 4 种类型需 2 位二进制($2^2=4$),总码长 = $2 \times 10000 = 20000$ 位(假设处理 1 万次)。
-
哈夫曼编码:
- 可回收物:1 位 × 4500 次 = 4500 位
- 厨余垃圾:2 位 × 3000 次 = 6000 位
- 有害垃圾:3 位 × 1500 次 = 4500 位
- 其他垃圾:3 位 × 1000 次 = 3000 位
- 总码长 = $4500 + 6000 + 4500 + 3000 = 18000$ 位。
-
节省比例:
- 节省位数 = $20000 - 18000 = 2000$ 位
- 节省比例 = $2000 / 20000 = 10\%$。
第三大题
3.1
动态规划求解最短路径步骤
- 找出最优解的性质,并描绘其结构特征。
- 递归的定义最优值。
- 以自底向上的方式计算出最优值,构造最优解。
3.2
建立状态转移方程
-
定义:
- $s$:当前节点
- $x$:节点 $s$ 的前驱节点
- $c(x, s)$:$x$ 到 $s$ 的边
- 转移方程分段函数: $$ f(s) = \begin{cases} 0 & \text{若 } s = 1 & \text{(起点)} \\ \min \big\{ f(x) + c(x, s) \big\} & \text{若 } s \neq 1 & \text{(其他节点)} \end{cases} $$
填表计算最优值
- $f[i]$:从节点 1 到节点 $i$ 的最短距离
- $p[i]$:节点 $i$ 的前驱节点
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| f[i] | 0 | 4 | 2 | 3 | 8 | 6 | 11 | 12 | 12 | 16 |
| p[i] | 0 | 1 | 1 | 1 | 3 | 4 | 4 | 5 | 6 | 9 |
最短路径长度及最优路线
- 最短路径长度:$f(10) = 16$。
- 路径:$1 \to 4 \to 6 \to 9 \to 10$。
第四大题
4.1
分治法
将 $X,Y$ 拆分为两半($k = n/2 = 4$ 位):
$A=1234$,$B=5678$,$C=5678$,$D=4321$
$X = A \times 10^k + B$,$Y = C \times 10^k + D$
$XY = AC \cdot 10^{2k} + (AD + BC) \cdot 10^k + BD$
乘法次数:4 次
4.2
算法优化
优化关键点:
$$ \begin{align*} (AD + BC) &= (AC + AD + BC + BD) - AC - BD \\ &= A(C+D) + B(C+D) - AC - BD \\ &= (A+B)(C+D) - AC - BD \end{align*} $$$XY = AC \cdot 10^{2k} + [(A+B)(C+D) - AC - BD] \cdot 10^k + BD$
乘法次数:$AC$、$BD$、$(A+B)(C+D)$
4.3
复杂度对比
- 优化前:$T(n) = 4T(n/2) + O(n)$,解得 $T(n) = O(n^2)$。
- 优化后:$T(n) = 3T(n/2) + O(n)$,解得 $T(n) = O(n^{\log_2 3}) \approx O(n^{1.585})$。
- 结论:优化后效率显著提升(指数级降低)。