离散数学

更新: 1/6/2025 字数: 0 字 时长: 0 分钟

• 考试题型：四道大题
• 时间：14:40 - 16:40
• 地点：西楼 - 507
• 监考老师：赵雪、程良

第一大题

灯泡L只有同时满足以下逻辑条件才会亮起：

• 如果 $S_1$ 闭合，则 $S_2$ 闭合
• 开关 $S_3$ 闭合
• 如果 $S_2$ 断开，则 $S_3$ 也断开

第一小题

命题的概念？以上三个条件都是命题吗？陈述句一定是命题吗？如果不是请举例。

• 命题是指可以被判断为真或为假的陈述句
• 都是命题
• 陈述句不一定是命题，例如：$x+3>5$ （$x$ 是变量，没有具体值，无法判断真假）

第二小题

将以上三个条件符号化，并写出灯泡 L 亮的判定公式。

设：$p$：$S_1$ 闭合、$q$：$S_2$ 闭合、$r$：$S_3$ 闭合

三个条件符号化：① $p\to q$、② $r$、③ $\neg q\to \neg r$

灯泡 L 亮的判定公式：$A=(p\to q)\wedge r\wedge (\neg q\to \neg r)$

第三小题

写出判定公式的真值表，并根据真值表写主范式。

$p$	$q$	$r$	$\neg q$	$\neg r$	$p\to q$	$\neg q\to \neg r$	$(p\to q)\wedge r$	$(p\to q)\wedge r\wedge (\neg q\to \neg r)$
0	0	0	1	1	1	1	0	0
0	0	1	1	0	1	0	1	0
0	1	0	0	1	1	1	0	0
0	1	1	0	0	1	1	1	1
1	0	0	1	1	0	1	0	0
1	0	1	1	0	0	0	0	0
1	1	0	0	1	1	1	0	0
1	1	1	0	0	1	1	1	1

由真值表可得，011 和 111 为成真赋值

故 $A=(p\to q)\wedge r\wedge (\neg q\to \neg r)\iff m_3\vee m_7$

第四小题

一阶命题逻辑符号化，用以下谓词描述三场景。

• $S(x)$：$x$ 是一个开关
• $L(x)$：$x$ 是一个灯泡
• $C(x,y)$：$x$ 与 $y$ 是连接的
• $P(x)$：$x$ 是闭合的
• $B(x)$：$x$ 是亮的

1. 所有开关都是可以控制灯泡的。

   $\forall x(S(x)\to \exists y(L(y)\wedge C(x,y)))$

2. 如果 $S_1$ 闭合，那么灯泡 $L_1$ 就会亮。

   $P(S_1)\wedge C(S_1,L_1)\to B(L_1)$

3. 如果 $L_1$ 与 $L_2$ 都亮，那么他们至少有一个共同开关。

   $B(L_1)\wedge B(L_2)\to \exists z(S(z)\wedge C(L1,z)\wedge C(L2,z))$

第二大题

对 60 个人的调查表明，有 25 人阅读《三联生活周刊》杂志，26 人阅读《读者》杂志，26 人阅读《中国国家地理》杂志，9 人阅读《三联生活周刊》和《中国国家地理》杂志，11 人阅读《三联生活周刊》和《读者》杂志，8 人阅读《读者》和《中国国家地理》杂志，还有 8 人什么杂志也不读。

第一小题

求阅读全部三种杂志的人数。

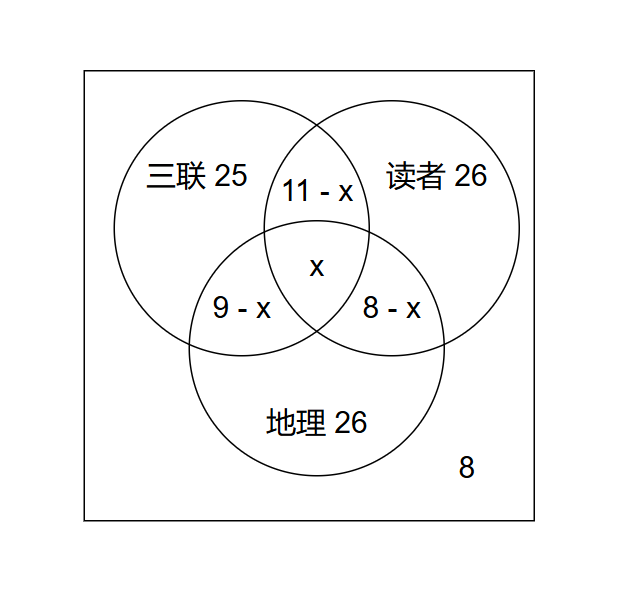
解：设三者共同有人数为 $x$，阅读三联与读者人数为 $(11-x)$ 人，读者与地理的人数为 $(8-x)$ 人，三联与地理的人数为 $(9-x)$ 人，因为 8 人什么也不读，所以 $60-8=52$ 人。

• 三联：$25-[(9-x)+x+(11-x)]=25-(20-x)=5+x$
• 地理：$26-[(9-x)+x+(8-x)]=26-(17-x)=9+x$
• 读者：$26-[(11-x)+x+(8-x)]=26-(19-x)=7+x$

$$\begin{array}{rl}(9+x)+(5+x)+(7+x)+(9-x)+(11-x)+(8-x)+x& =52\\ 49+x& =52\\ x& =3\end{array}$$

答：阅读全部杂志的人数为3人

第二小题

分别求只阅读《三联生活周刊》《读者》和《中国国家地理》杂志的人数。

解：由上题可知

三联人数：$x+5=3+5=8$ 人

读者人数：$x+7=3+7=10$ 人

地理人数：$x+9=3+9=12$ 人

综上三联人数 8 人，读者人数 10 人，地理人数 12 人。

第三大题

五个学生 a，b，c，d，e

a 关注 b 的社交账号，b 关注 c，c 关注 d，d 关注 a，e 关注 b。

第一小题

写出这几个同学的集合。

$A=\{a,b,c,d,e\}$

第二小题

写出二元关系中的有序队，例如 a 关注 b 写为 $<a,b>$。

$R=\{<a,b>,<b,c>,<c,d>,<d,a>,<e,b>\}$

第三小题

画出二元关系的关系图，判断该关系是否有自反性，对称性，传递性。

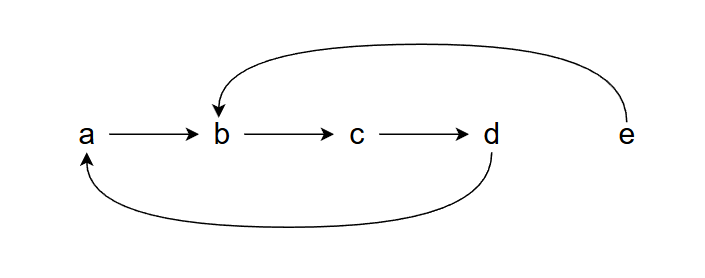
没有自反性，没有对称性，没有传递性。

第四小题

写出还关系的自发闭包、对称闭包、传递闭包。

自反闭包：

$$\begin{array}{rl}s(R)=\{& <a,a>,<b,b>,<c,c>,<d,d>,<e,e>,\\ & <a,b>,<b,c>,<c,d>,<d,a>,<e,b>\}\end{array}$$

对称闭包：

$$\begin{array}{rl}r(R)=\{& <a,b>,<b,a>,<b,c>,<c,b>,<c,d>,\\ & <d,c>,<d,a>,<a,d>,<e,b>,<b,e>\}\end{array}$$

传递闭包：

$$\begin{array}{rl}t(R)=\{& <a,a>,<a,b>,<a,c>,<a,d>,\\ & <b,a>,<b,b>,<b,c>,<b,d>,\\ & <c,a>,<c,b>,<c,c>,<c,d>,\\ & <d,a>,<d,b>,<d,c>,<d,d>,\\ & <e,a>,<e,b>,<e,c>,<e,d>,\}\end{array}$$

第五小题

a，b，c 上台领奖，奖品有 A、B 两种，可以怎样分配这些奖品。

设：$L=\{a,b,c\}$，$X=\{A,B\}$ 求 $X^L$

解：$X^L=\{f_0,\dots ,f_7\}$

$$\begin{array}{rl}{f}_0& =\{<a,A>,<b,A>,<c,A>\}\\ f_1& =\{<a,A>,<b,A>,<c,B>\}\\ f_2& =\{<a,A>,<b,B>,<c,A>\}\\ f_3& =\{<a,A>,<b,B>,<c,B>\}\\ f_4& =\{<a,B>,<b,A>,<c,A>\}\\ f_5& =\{<a,B>,<b,A>,<c,B>\}\\ f_6& =\{<a,B>,<b,B>,<c,A>\}\\ f_7& =\{<a,B>,<b,B>,<c,B>\}\end{array}$$

第四大题

某城市因空气严重污染出台了汽车数字单、双号限行政策分析一下问题。

第一小题

结合题写出单双号限行的等价关系 $R$ 的集合定义，阐述等价关系定义，求解各尾号的的等价类。

解：汽车尾号集合

$A=\{0,1,2,3,4,5,6,7,8,9\}$

$R=\{(x,y)|x,y\in A\wedge x\equiv y(mod2)\}$

$R$ 是 $A$ 上的等价关系，则 $R$ 满足以下三个条件。

• $R$ 满足自反性：对于 $x\in A$，均有 $<x,x>\in R$

• $R$ 满足对称性：对于所有 $x,y\in A$，如果 $<x,y>\in R$，则 $<y,x>\in R$

• $R$ 满足传递性：对于所有 $x,y,z\in A$，如果 $<x,y>\in R$，且 $<y,z>\in R$，则 $<x,z>\in R$

• 汽车尾号各数字等价类

$$[1]=[3]=[5]=[7]=[9]=\{1,3,5,7,9\}$$$$[0]=[2]=[4]=[6]=[8]=\{0,2,4,6,8\}$$

第二小题

编写模块化程序，实现等价关系判定，假设关系用一个 n*n 矩阵 $R=(rij{)}_{n\times n}$ 表示。可定义一个 n*n 数组 r[n][n] 表示矩阵关系，根据题意补全算法。

r[i][i] == 1
r[i][j] == r[j][i]
r[i][j] && r[j][k] && !r[i][k]
checkzifan() && checkduichen() && checkchuandi()

贡献者

wkwbk

页面历史

最后编辑于 15 天前

查看完整历史

af0b5b3-🎉 init: 项目初始化