算法分析与设计

更新: 6/29/2025 字数: 0 字 时长: 0 分钟

• 时间：10:30 - 12:30
• 地点：中心楼 612-614
• 监考老师：杨晓明、肖琼谞

第一大题

情景

分支限界法与回溯法（环保方案投资问题）

题目背景

有 3 个环保投资方案：

• 方案 1：成本 16 万元，减碳量 45 万吨
• 方案 2：成本 15 万元，减碳量 25 万吨
• 方案 3：成本 15 万元，减碳量 25 万吨

总投资成本上限 30 万元，目标是最大化总减碳量。

1.1

分支限界法和回溯法的区别及相同点？

求解目标不同：

• 回溯法的求解目标是找出解空间树中满足约束条件的所有解
• 分支限界法的求解目标是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解

搜索方式不同：

• 回溯法以深度优先的方式搜索解空间树
• 分支限界法以广度优先或以最小耗费优先的方式搜索解空间树

相同点：

• 均基于解空间树搜索；采用剪枝优化搜索效率。

1.2

数学建模。

1. 问题转化：将环保投资问题建模为 0-1 背包问题模型。
2. 变量定义：$x_i\in \{0,1\}$ 表示是否投资第 $i$ 个方案（1=投资，0=不投资）。
3. 目标函数：最大化总减碳量 $max\sum _{i=1}^3{v}_i{x}_i$（$v_i$ 为减碳量）。
4. 约束条件：总成本 $\sum _{i=1}^3{w}_i{x}_i\le 30$（$w_i$ 为成本）。
5. 结论：减碳量等效为背包"价值"，成本等效为"重量"，投资上限 30 等效为背包容量。

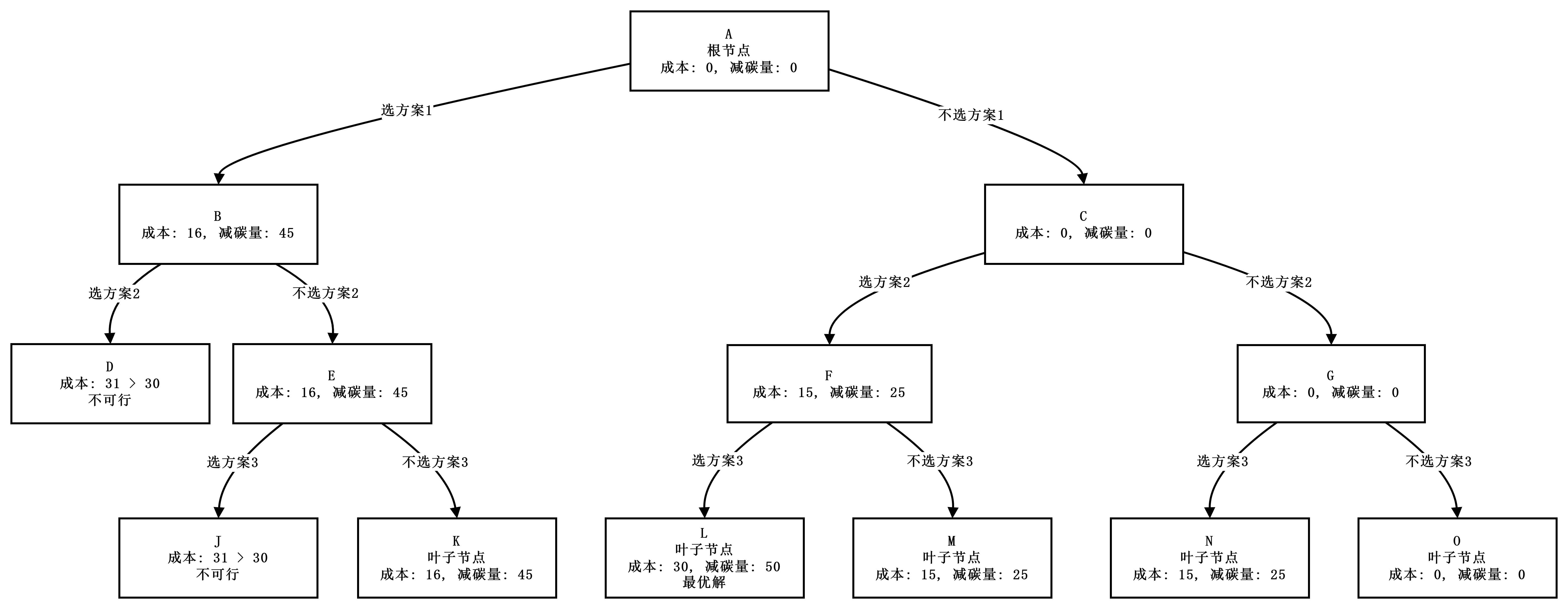
队列式分支限界法求解过程？最大减碳量？最优方案组合？

1. 构造解空间树：三层二叉树（左分支=选方案，右分支=不选方案）。

2. 搜索过程：

   [A] B, C        => B, C
   [B, C] D, E     => E
   [C, E] F, G     => F, G
   [E, F, G] J, K  => K(45)[1,0,0]
   [F, G] L, M     => L(50)[0,1,1], M(25)[0,1,0]
   [G] N, O        => N(25)[0,0,1], O(0)[0,0,0]

3. 最优值（最大减碳量）：50 万吨

4. 最优解（最优方案组合）：选方案 2 和方案 3，即 $x=[0,1,1]$

1.3

回溯法编程实现，找这个方案的最大减碳量以及最优方案组合。

回溯函数

void Backtrack(int i) {
    // 如果到达叶子节点
    if (i > n) { 
        bestp = cp; 
        return; 
    }

    // 进入左子树
    if (cw + w[i] <= c) {
        cw += w[i];
        cp += p[i];
        Backtrack(i + 1);
        cw -= w[i];
        cp -= p[i];
    }

    // 进入右子树
    if (Bound(i + 1) > bestp) {
        Backtrack(i + 1);
    }
}

限界函数

private static double Bound(int i) {
    // 计算剩余容量
    double cleft = c - cw;  

    double bound = cp;

    // 以物品单位重量价值递减序装入物品
    while (i <= n && w[i] <= cleft) {
        cleft -= w[i];
        bound += p[i];
        i++;
    }

    // 装满背包
    if (i <= n) {
        bound += p[i] / w[i] * cleft; 
    }

    return bound;
}

第二大题

情景

贪心算法（哈夫曼编码应用）

题目背景

对 4 类垃圾编码，出现频率：

编号	垃圾类型	频率
1	可回收物	45%
2	厨余垃圾	30%
3	有害垃圾	15%
4	其他垃圾	10%

2.1

贪心算法的原理是什么？

• 贪心算法是一种通过局部最优选择来构建全局最优解的算法。
• 它依赖于贪心选择性质和最优子结构，即每一步都选择当前最优，期望最终得到全局最优解，且无需回溯。

哈夫曼编码原理是什么？

1. 变长编码：哈夫曼编码是一种变长编码方式。出现频率高的字符分配较短的编码，出现频率低的字符分配较长的编码。

2. 频率排序：首先将字符按照出现频率从小到大排序。

3. 构造哈夫曼树：

   • 每次选取频率最小的两个节点。
   • 创建一个父节点，其频率等于这两个子节点频率之和。
   • 将该父节点按照频率大小重新插入到排序好的节点队列中。
   • 重复以上步骤，直到队列中只剩下一个节点，这个节点就是哈夫曼树的根节点。

4. 编码：在哈夫曼树上，左分支编 0 右分支编 1，直到到达叶子节点，路径上的 0 和 1 组成的字符串就是该字符的哈夫曼编码。

定长编码的原理是什么？

定长编码也称为等长编码，是一种数据编码方式，其中每个字符或符号都用固定长度的二进制位来表示。

定长编码计算方式：

1. 确定字符集大小 $N$（需编码的不同字符总数）。

2. 计算最小编码位长 $L$：$2^L⩾N$

   • 等价对数形式：$L=\lceil {\log }_{2}N\rceil$，其中 $\lceil \cdot \rceil$ 表示向上取整函数。

2.2

构造哈夫曼树及编码，写出具体的构造过程，写出每种垃圾名称的具体编码。

垃圾类型由小到大排序：

4	3	2	1
其他垃圾	有害垃圾	厨余垃圾	可回收垃圾
10%	15%	30%	45%

构造哈夫曼树：

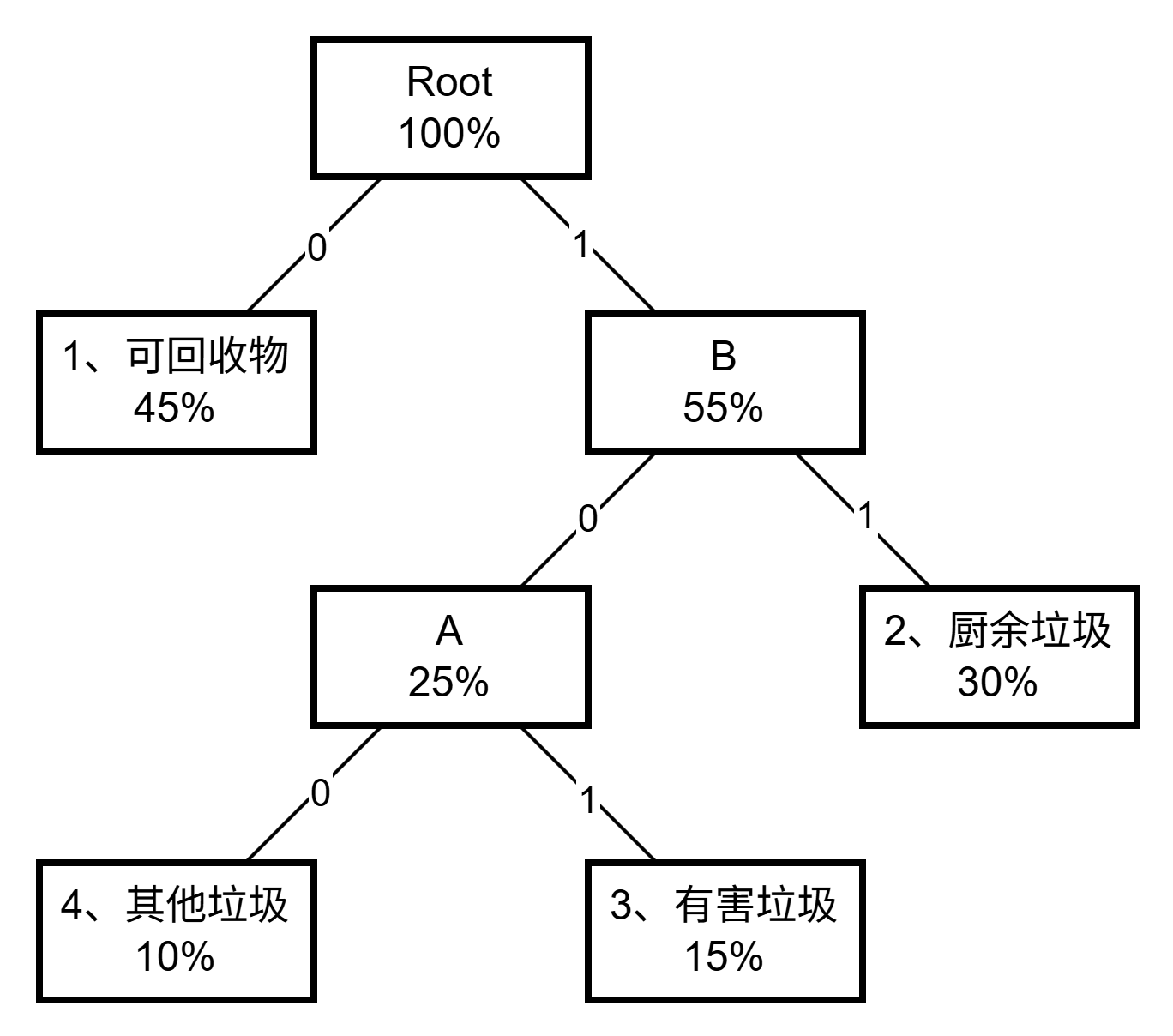
根据哈夫曼树可得：

• 可回收物：0
• 厨余垃圾：11
• 有害垃圾：101
• 其他垃圾：100

2.3

编码长度与节省比例计算

1. 定长编码：
   • 4 种类型需 2 位二进制（$2^2=4$），总码长 = $2\times 10000=20000$ 位（假设处理 1 万次）。
2. 哈夫曼编码：
   • 可回收物：1 位 × 4500 次 = 4500 位
   • 厨余垃圾：2 位 × 3000 次 = 6000 位
   • 有害垃圾：3 位 × 1500 次 = 4500 位
   • 其他垃圾：3 位 × 1000 次 = 3000 位
   • 总码长 = $4500+6000+4500+3000=18000$ 位。
3. 节省比例：
   • 节省位数 = $20000-18000=2000$ 位
   • 节省比例 = $2000/20000=10\mathrm{\%}$。

第三大题

情景

动态规划（多阶段决策问题）

题目背景

求图 3-16 中节点 1 到 10 的最短路径（边权已知）。

3.1

动态规划求解最短路径步骤

1. 找出最优解的性质，并描绘其结构特征。
2. 递归的定义最优值。
3. 以自底向上的方式计算出最优值，构造最优解。

3.2

建立状态转移方程

1. 定义：
   • $s$：当前节点
   • $x$：节点 $s$ 的前驱节点
   • $c(x,s)$：$x$ 到 $s$ 的边
2. 转移方程分段函数：$$f(s)=\{\begin{array}{lll}0& \text{若 }s=1& \text{(起点)}\\ min\{f(x)+c(x,s)\}& \text{若 }s\ne 1& \text{(其他节点)}\end{array}$$

填表计算最优值

• $f[i]$：从节点 1 到节点 $i$ 的最短距离
• $p[i]$：节点 $i$ 的前驱节点

	1	2	3	4	5	6	7	8	9	10
f[i]	0	4	2	3	8	6	11	12	12	16
p[i]	0	1	1	1	3	4	4	5	6	9

最短路径长度及最优路线

1. 最短路径长度：$f(10)=16$。
2. 路径：$1\to 4\to 6\to 9\to 10$。

第四大题

情景

分治法（大整数乘法）

题目背景

用分治法计算两个 8 位数乘法（如 $X=12345678$，$Y=56784321$)。

4.1

分治法

将 $X，Y$ 拆分为两半（$k=n/2=4$ 位）：

$A=1234$，$B=5678$，$C=5678$，$D=4321$

$X=A\times {10}^k+B$，$Y=C\times {10}^k+D$

$XY=AC\cdot {10}^{2k}+(AD+BC)\cdot {10}^k+BD$

乘法次数：4 次

4.2

算法优化

优化关键点：

$$\begin{array}{rl}(AD+BC)& =(AC+AD+BC+BD)-AC-BD\\ & =A(C+D)+B(C+D)-AC-BD\\ & =(A+B)(C+D)-AC-BD\end{array}$$

$XY=AC\cdot {10}^{2k}+[(A+B)(C+D)-AC-BD]\cdot {10}^k+BD$

乘法次数：$AC$、$BD$、$(A+B)(C+D)$

4.3

复杂度对比

1. 优化前：$T(n)=4T(n/2)+O(n)$，解得 $T(n)=O(n^2)$。
2. 优化后：$T(n)=3T(n/2)+O(n)$，解得 $T(n)=O(n^{{\log }_{2}3})\approx O(n^{1.585})$。
3. 结论：优化后效率显著提升（指数级降低）。

总结

贡献者

LI SIR

页面历史

最后编辑于 9 天前

查看完整历史

6cfb6ce-docs: 更新算法分析与设计考试笔记

eb3d1cc-docs: 更新算法分析与设计考试笔记

634b87f-docs: 更新算法分析与设计考试笔记

1788f78-docs: 更新算法分析与设计考试笔记

e31b9a5-docs: 更新各科考试笔记的总结

8e63a8c-docs: 更新考试笔记

5581cd4-docs: 更新“机器学习”和“算法分析与设计”考试的考场和监考老师

9eb0366-docs: 交换机器学习和算法分析考试日期

a1a3196-docs: 更新算法分析与设计考试笔记

fff0298-docs: 更新算法分析与设计考试笔记

6573486-docs: 更新算法分析与设计考试笔记

4c032a9-docs: 添加目录

46e57e2-docs: 更新所有考试科目的监考老师

5fdb1e5-docs: 更新考试位置和格式索引

28219f1-Refactor: 重命名 XASYU 考试目录并更新导航

053f56e-Refactor: 调整考试日期